
Contrastive Representation Learning — A Comprehensive Guide (part 1, foundations)
Turns out, telling things apart is a good way to understand the world
Nobody likes labels. Specifically with regards to machine learning, the modus operandi of most models is to take in batches of data elements and their associated labels (“cat”, “road pixel”, “adjective” etc.) to learn a mapping, such that when new data elements are presented, they can be put into one of the labels used during the training phase.

Such a neat mapping from data elements to labels has many benefits in industry, allowing for automation or augmentation of many workflows traditionally performed by tedious human labor (such as counting customers entering a grocery store or figuring out what kinds of vehicles are in a parking lot) without a major system redesign. I love bar charts as much as the next person, but such models are inherently limited to their narrow operating schema. It is tough to expand their capabilities to new tasks and use them for anything other than what they were designed for. Humans by contrast can create new cateogories on the fly and use context to describe something in a variety of ways.
Why is this the case? The shortlist of issues that traditional supervised deep learning models suffer from:
- They assume that classes seen during training represent the universe of all possible classes of data elements — thus they do not adapt to seeing completely new data classes (out of sample generalization)
- They need tremendous amounts of existing data to learn useful representations, which is laborious at best and impossible at worst — for example when the class is rare in the real world (sample efficiency problem)
- They cannot easily be retrained on new data without degrading existing task performance (catastrophic forgetting)
- They cannot learn anything from the vast amount of unlabeled data that is created everyday (supervision problem)
These are also more broadly the major open problems in machine learning as a whole. Representation learning does not solve all of these problems, but it provides a good framework and a way of thinking about machine learning tasks that alleviates many of these issues. Here’s an attempt at defining it:
Representation learning is the task of extracting useful, compressed representations of labeled or unlabeled data elements so that they can be used in a wide number of downstream tasks.
In many ways, the definition above is unsatisfactory. This is really the goal of most deep learning as a whole - learning good features. However, two parts of this definition serve to accurately portray important elements of the field: learning from both labeled and unlabeled data and learning representations that are broadly useful. The no-free lunch theorem may immediately come to mind here for experienced readers, but there is a big chasm between being SOTA on all possible tasks and being perfect at one at the expense of all others. That chasm may contain the subset of being good at “all useful tasks” from the viewpoint of our universe, and so it is definitely worth pursuing.
Contrastive learning on the other hand is more so a training methodology for machine learning models (so should more accurately be called contrastive training), that just so happens to be extremely useful in learning such robust representations. The research area of representation learning as a whole is vast, and this article will focus on depth instead of breadth, aiming to understand the narrower area of Contrastive Representation Learning through implementation and applied case studies. The bright side of this is that some of the most powerful methods out there in representation learning are contrastively trained models (SimCLR, MoCo, SimSiam etc.), so the method has a good amount of promise as it stands.
Additionally, this article will focus on implementations from scratch. This means that basic knowledge of Pytorch best practices and general functioning is needed. It is best to come into this from a beginner-intermediate standpoint, where you’ve likely written a few basic dataloaders, coded at least a simple model using modules and sub-modules, and written several training and inference loops. The following situations will be encountered through this article:
- Non-equal batch sizes
- Custom sampling strategy
- Multiple forward passes
- Manual control of CPU and GPU storage of tensors during training
- Custom tensorboard hooks
The focus will be on computer vision tasks, so a good GPU (4GB+) is absolutely needed.
Table of contents:
- Contrastive Learning: Background
- What is Similarity?
- Dataloaders and Sampling Strategy
- Model Architecture
- Writing a Contrastive Trainer
- Loss Functions and Exemplar Mining
- Evaluating Representation Learning Models
The finished version of all of the code in this article is available at this repo.
Contrastive Learning: Background
Key concept: Contrastive models seek to quantify the similarity or dissimilarity between data elements.
Contrastive models and training techniques have enjoyed a long and varied history within machine learning. One of the first notable examples, while not termed under the exact term “contrastive learning” was published in 1993 in fact, and used for a signature verification task. Following this the task of interest became person re-identification, and then more broadly few-shot or one-shot learning on datasets like Omniglot. However, uses have also existed in text embedding, with modifications to word2vec utilizing one of the earliest forms of true contrastive loss. To understand these use cases, we need to first understand what having such a model would allow you to do. Think about a machine that can take in two elements and produce a similarity score:

Signature verification is easy to think about in this way, if a check claims to have a signature from a particular person we can put the check’s signature into the machine with a known signature from the person and see what the similarity looks like. For tasks like this simple subtraction of the images doesn’t work, and even more complex patch comparison methods like * suffer from the huge variety of contexts that natural images contain. The benefit of using deep learning models for this task is representation power, they can learn feature spaces in which only the most distinctive portions of images are represented, allowing similarity to be better determined. The usage of deep learning models to build such representations is called deep representation learning, or depending on your school of thought, deep metric learning. Thus, for deep learning models (and many traditional machine learning models also) the workflow looks more like the following:

The deep learning model, M, converts input data elements into a vector space in which similar examples have similar vector representations, and different examples have distinct vector representations. The S here could correspond to a single dot product or Cosine similarity — the key is that the vectors extracted using the deep learning model highlight attributes that are causing the objects to be similar (or dissimilar).
Key concept: Deep learning models have revolutionized representation and metric learning because of their ability to extract key semantic attributes from large datasets
Most readers familiar with deep learning will now jump immediately to the loss function — how can we encourage the model to form representations with this property? The answer is surprisingly simple (relatively, of course):

This is one of the simplest loss formulations for contrastive learning. In the equation above the indication function Sxy is equal to 1 if x and y are similar and zero otherwise. So when the examples are similar we are trying to minimize the distance between them, and when they’re dissimilar we’re trying to minimize their distance from a margin. But what the hell is a margin?
It would be unfair to say it is anything more than a logistical convenience. We need places in our vector space to place our representations, and what we’re saying with this loss function is let’s place representations of similar images into the same place, and put representations of dissimilar images anywhere such that they’re margin distance away. This will have some unintended consequences down the line, and we will explore these in some of our experiments with different loss functions. For now, it’s important to know that we can directly encourage the model to have vector representations that are far apart when inputs are dissimilar and vice versa.
We also need to be more specific when we say two elements are “similar” or “dissimilar”. For images, we can say two images X,Y are similar if they contain the same object — however this requires the same amount of supervision as simple image classification (we can simply put all similar images together and recover the class grouping). So what good are contrastive models in the setting where similarity is determined by (known) image content?
Well in some cases (such as person re-identification), we may know the class label of the image (who is in the image) but we have many more classes than examples per class — we may only have an image or two of a person but several thousand persons in our database. This leads to many problems for traditional classifiers which would try to predict person identity given image, as there is a very small amount of within class variability (zero in the case of a single image) to learn discriminitive features to predict the class from. Contrastive models by comparison are learning features to help distinguish between classes, and as such can learn from at least (C-1) examples given C total classes and an image from a particular class. Additionally, there may be classes present during test time that we haven’t seen during training, and a traditional classifier would have to assign these to one of the training classes. By comparison, the contrastive model can evaluate pairwise similarity between all testing example and discover new “clusters” of similar images that would correspond to new classes.
However, the magic of representation learning comes into play when labels are not present. It is much easier to ascertain similarity in an automatic way vs. trying to ascertain exact content or pixel labels? Confused yet? Read on.
What is Similarity?
Consider the following, if you took a picture of your cat (which you definitely have, given you’re reading this article) and used an image editing program to flip it over the center line, would that change the content of the picture?
No, you would still maintain that the image is of the same cat. Likewise if you blurred the picture a bit, or cropped out a border. Such operations preserve the semantics, or main content, of the image. From most people’s definition of similar than, the original image and the image with one of these semantics preserving transforms would be deemed “similar”. Notice what we did here? We were able to create a pair of similar images without having to explicitly tag the content or pixels of the image with a label.
Key concept: We can automatically create pairs of similar images by applying a semantics preserving transform (such as a flip, blur, or random crop) — without ever seeing or labeling the image
This is not as easy to do when your examples are from other modalities such as sound or text. For example, in text we can either use strict similarity using something like a curated synonym lookup, or we can be a little more flexible and use contextual similarity (i.e two words are similar if they commonly occur in close proximity). This has important implications for the learned representations, as “fish” and “whale” are not synonyms but will likely be commonly co-occuring. We need to think a bit about whether we want such terms to have similar representations.
In general, these techniques fall under the umbrella of self-supervised learning, which focuses on generating a supervision signal automatically from the data. There’s many different approaches to this, and it’s a great way of pre-training models against the nearly unlimited amounts of unlabeled data out there. For this post we will start by defining similarity as images belonging to the same (known) class, then transition into a fully unsupervised approach using images without class labels. Let’s get started.
Dataloaders and Sampling Strategy
We will build two dataloaders for our use case, one for when we are using labeled data (i.e images are organized into folders that correspond to their label) and one for when we are using unlabeled data (i.e all the images are in a single folder and their class unknown).
For the supervised case, we first outline our sampling strategy. Remember we need to output a dictionary of similar pairs of datapoints. For now we will assume each folder (named for the class of images it contains) has more than one image. We can then sample a pair of images from each folder and simply organize them into rows of a tensor. We will index all the images as a whole, so the sampling strategy becomes:
- Get the indexed example, figure out what class it’s from (i.e parent folder)
- Sample another image from that class to form a pair
- Go through all other classes and sample pairs of images from each class
This leads to the following Pytorch dataset:
This dataset outputs a dictionary containing a BxCxHxW tensor for “x1” — these are anchor images, a BxCxHxW tensor for “x2 — these are the similar (same class in our case) examples to x1, and a Bx1 tensor for “labels” — these are the ground truth class of the pair.
One tricky thing is that we will be constructing the batches within the dataset itself, so if we pass this to the DataLoader constructor we need to specify batch_size = None. That way we can assure that each batch contains exactly one pair from each class and help prevent imbalances from random sampling. This will actually become easier in the unsupervised/self-supervised case, as we will simply assume each image is its own class. For now the batch size is fixed at C, the number of classes.
The “labels” here are simply for visualization and evaluation later on.
We will be able to re-use this class to generate contrastive pairs over any dataset that is organized into folders by classes (i.e the “ImageFolder” format from Pytorch)
Key concept: Each batch element will be an “anchor” image and another image that forms a similar pair
Model Architecture
We can be pretty flexible with our model architecture. We need to keep in mind however that most models come built in with a “prediction head” i.e a fully connected layer or something similar that generates the actual predictions for a specialized task. Since we are looking to more broadly learn representations, the prediction head will be an unneeded compression to a usually low-dimensional space. For our purposes it will be helpful to think of a model as consisting of a backbone (which will extract the representations we need), a “projector” (which will essentially filter the features learned through the backbone for a specialized task), and a “head” (which will use the filtered features from the projector to generate a prediction). For example study the architecture below, which is a model used for generating a binary prediction given an input image with a single channel:
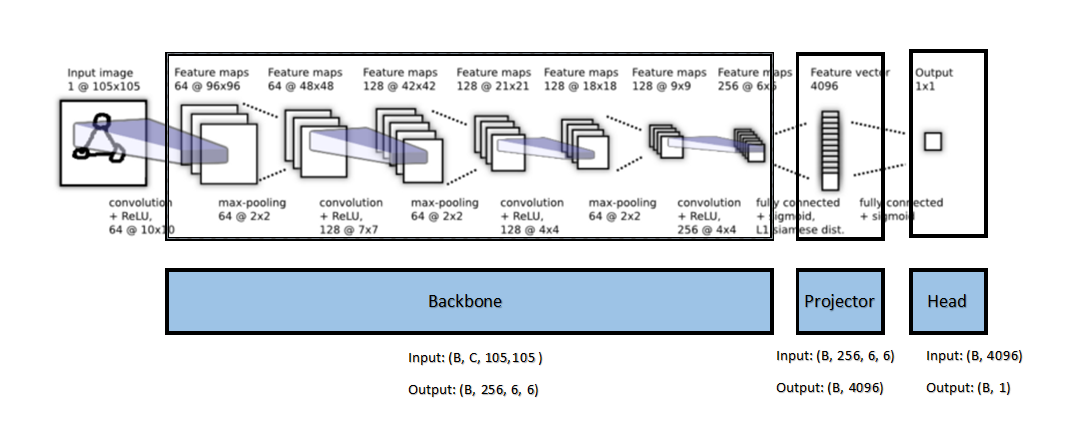
The torchvision library has many different model architectures we can use instead of creating them layer-by-layer. For our experiments we will use a simple Resnet-18 model with the head repurposed as a simple projector. The code to do this is simply:
from torchvision import models
EMB_SIZE = 2embedding_net = models.resnet18()
embedding_net.conv1 = nn.Conv2d(1, 64, (7,7), (2,2), (3,3))
embedding_net.fc = nn.Linear(512, EMB_SIZE)
model = embedding_net
model.train(); print()
Notice in addition to changing the output dimension of the fully connected head to the desired size of our embeddings, we also alter the first convolutional layer to take in images with 1 channel instead of 3 channels (this is required since MNIST images are 1 channel). We’re using EMB_SIZE = 2 here to make it easier to visualize the embeddings, however in practice this is usually set to higher values such as 128 or 256.
That concludes all that is needed to set up the actual model architecture. We will handle the rest of the heavy lifting within the Trainer and Loss modules.
Training a Contrastive Model
We have data and we have a model, there’s only two elements remaining until we’re clear to start training: a trainer, and a loss function. The trainer will implement the forward and backward pass through the model, update the model parameters, and log results. We will start by creating a skeleton of the trainer with a method for training a single iteration (forward pass + loss calculation + backward pass) and a method for training a set number of epochs.
This trainer is generic enough to be used with pretty much any pytorch model, and we’ll need to add some extra features to customize it for a contrastive training framework.
Firstly, recall we have a pair of examples for each batch element, so we’ll need to pass this through the model in sequence to get the respective embeddings. We can do this by altering train_iter() to do two passes through the model.
x1, x2 = input
out1 = model(x1); out2 = model(x2)Next, we’ll need to extract the elements individually from the data_dict in the train() method to send them to the current device:
## Grab an example
x1 = data_dict["x1"]; x2 = data_dict["x2]
label = data_dict["label"]## Send it to self.device
x1 = x1.to(self.device); x2 = x2.to(self.device)
label = label.to(self.device)x = (x1,x2)
Lastly, the loss function (that we’ll write soon) will take both output embeddings to calculate the distance between them. We can alter this within the train_iter() method:
## Calculate the loss(es)
loss = self.loss_function(out1, out2)The finalized trainer looks like this:
Loss Functions and Negative Mining
This is probably one of the most important components of contrastive methods, next to data augmentation / sampling strategy. Before we go over the deep end we’ll start with the simple Margin Loss — the same one we saw earlier in this post:

The margin loss starts by taking two data examples (x,y) along with a similarity label (Sxy) that is 1 when (x,y) are similar and 0 otherwise. Make sure you understand what minimizing this loss means — since D(x,y) is calculated by the network, the loss is minimized when D(x,y) is small at the same time that (Sxy) is 1 (i.e the network is representing known similar pairs in the same way). Conversely, to prevent the network from representing every example the same way (a phenomena known as collapse which we will discuss later on) we also force the model to represent dissimilar examples differently, by saying they should be seperated by alteast a margin distance of M.
Now recall our dataloader outputs two BxCxWxH arrays, containing similar examples in corresponding rows. The schema broadly looks like this:

but for the Contrastive Pair loss (and Triplet Loss) we need negatives as well, something that looks more like the following:

the easiest way to do this is for a given row in the anchor column, we take all non-corresponding rows in the positive column. This works because we only sample each class once and thus the only similar example to each anchor is in its corresponding row.
While not the quickest way, we can do this by repeating each index A sequentially N times and repeating index B batch-wise N times — this forms an array where none of the indexes are the same and we can then use it to index the batches into one large batch that is B*(B-1)xCxHxW — this is all possible similar and non-similar pairs along with a B*(B-1) label vector for similarity.
def form_pairs(inA, inB):
'''
Form pairs from two tensors of embeddings. It is assumed that the embeddings at corresponding batch positions are similar
and all other batch positions are dissimilar
i.e inA[i] ~ inB[i] and inA[i] !~ inB[j] for all i =! j
'''
b, emb_size = inA.shape
perms = b**2
labels = [0]*perms; sim_idxs = [(0 + i*b) + i for i in range(b)]
for idx in sim_idxs:
labels[idx] = 1
labels = torch.Tensor(labels)
return(inA.repeat(b, 1), torch.cat([inB[i,:].repeat(b,1) for i in range(b)]), labels.type(torch.LongTensor).to(inA.device))This will yield the following schema:

The overall loss function looks like the following:
We will implement the forward_triplets() and forward_ntxent() methods in the next sections.
Now that we have a dataloader, model, trainer, and loss function we can start training! We will use a small subset of 3000 examples from the larger MNIST training set (using SubsetRandomSampler) and see what our training dynamics look like. Then we will use a handful of unseen examples to visualize the embedding space. We will use an embedding size of 32 and use PCA to reduce them to 2 dimensions for visualizations. Below is a training notebook implementing all of the functions from above to train with Contrastive Pair loss:
Here’s a graph of training loss over our subset of 2000 examples for 10 epochs:

Here’s the resulting 2-dimensional PCA projections of the 32-dimensional test set embeddings (45% variance explained):

From just about 2,700 examples (90% of 3,000) we’ve learned embeddings that show great separation between digits. Let’s dig a bit into the math to figure out how many examples were actually compared. Firstly, for discriminatory models (where we’re predicting the digits directly) we would’ve had approximately 2700/10 = 270 examples per digit to learn the representation from. For contrastive learning, each batch contained one similar example of a digit and 9 dissimilar pairs- that means 10 comparisons per batch. Given 270 total batches that means each digit had 2700 comparisons made to learn the representation from. That’s 10x the number of examples to base a digit’s representation from compared to discriminatory methods.
Let’s dig into other loss functions to see if we can do even better. Firstly, notice with the Margin Loss we’re forcing the distance between similar examples to be 0. Since our sampling strategy forced only a single similar example per batch this isn’t so bad, but with a sampling strategy with balanced similar and dissimilar examples per class the similar examples will all start bunching together in small clusters. We’re trying to encode similar examples, but we’re treating them as if they should be the same example! This discourages intra-class variance, and we need to give the model room to place similar examples close together without placing them directly on top of each other (all 1’s . One way we can get around this (and the problem of setting the margin value, which itself is tricky) is to enforce a separate constraint. Instead of having the similar distance go to 0 and the dissimilar distance go to a margin, we can enforce the weaker constraint that similar distances are less than dissimilar distances across a batch.
The triplet loss utilizes this constraint:

In this formulation A is an (embedded) data point, P is another (embedded) data point that is similar to A, and N is another (embedded) data point that is dissimilar to A. In proper contrastive learning parlance these are known as the anchor, positive, and negative examples.
Luckily for us the Triplet Loss is already available as a Pytorch module. All we need to do is to add a function to form triplets from our batch:
def form_triplets(inA, inB):
'''
Form triplets from two tensors of embeddings. It is assumed that the embeddings at corresponding batch positions are similar
and all other batch positions are dissimilar
i.e inA[i] ~ inB[i] and inA[i] !~ inB[j] for all i =! j
'''
b, emb_size = inA.shape
perms = b**2
labels = [0]*perms; sim_idxs = [(0 + i*b) + i for i in range(b)]
for idx in sim_idxs:
labels[idx] = 1
labels = torch.Tensor(labels)
labels = labels.type(torch.BoolTensor).to(inA.device)
anchors = inA.repeat(b, 1)[~labels]
negatives = torch.cat([inB[i,:].repeat(b,1) for i in range(b)])[~labels]
positives = inB.repeat(b, 1)[~labels]return(anchors, positives, negatives)
then add the relevant forward method to our loss function:
Then we can start training just as before. All we need to do is specify “triplets” instead of pairs in our contrastive loss function.
Here’s the notebook training with Triplet Loss:
Here’s the training loss curve:

Here’s the resulting 2-dimensional PCA projections of the 32-dimensional test set embeddings (56% variance explained):

We can immediately notice that each of the individual clusters is now more “smeared out” — while this doesn’t immediately look like a good thing this allows the model to be more expressive with class separation. For example, if our dataset involved cats and dogs we may have images that contain a person or a plant in the background. Thus a cat picture with a person in the background should be closer to a dog picture with a person in the background compared to say, a picture of just a dog’s face. With Margin Loss these images would all be separated uniformly into tight clusters of margin distance.
We will explore one more loss function in this part, the NT-Xent (or Normalized Temperature Cross-Entropy) loss. This loss was introduced in the popular SimCLR paper and based off the Multi-class N-pair Loss (introduced in this paper). We will attempt to understand this loss via a few progressive steps. First, consider (for a single example) the common Cross Entropy loss for classification problems:

Given y being the ground truth label vector and yhat the predicted probability vector over the classes, this essentially boils down to the negative logarithm of the predicted probability for our class of interest. This value shrinks as the value of yhat goes to 1 and vice versa — the loss is minimized when we predict our class of interest with a probability of 1 and maximized when we predict the wrong class with a probability of 1.
Now, for a triplet a, p, n, the Multi-class N-pair Loss can be written (using some algebra) as:

where <x, y> denotes the inner product. Notice, just like Triplet Loss the denominator will increase as the distance between an anchor-positive and anchor-negative embedding increases. We can treat the distances similar to the probability in the Cross Entropy loss — we’d like to separate dissimilar examples with the most distance. With some more algebra, we can rewrite it as the following:

Finally, if we have only one similar example per class in our data batch we can re-write it as the following, where instead of using an explicit negative to the anchor in the denominator we iterate over all non-corresponding indices in the batch.

For a more through explanation of the NT-Xent loss check out the following guides here, here, and here. The implementation here borrows heavily from the last link.
Our finalized loss function with pairs, triplet, and NT-Xent integrated looks like the following:
and the training notebook for NT-Xent loss:
The progression of the training loss:

Here’s the resulting 2-dimensional PCA projections of the 32-dimensional test set embeddings (35% variance explained):

Finally, we will use a simple baseline by training with the classic Cross-entropy function directly against the labels.
The resulting embeddings look like the following and have the highest % variance explained by PCA: 80% — this suggests that a large number of the 32 features are collinear. We will explore this point more in the next section.

The Effects of Different Loss Functions
Using the same batch size, # of training examples, sampling strategy, and hyperparameters we get the following embeddings:

What’s going on here? It seems like Triplet loss does the best job visually of separating the classes, but this is not nearly the full story. For example, it is easy to forget that these are 2-dimensional projects of 32-dimensional points, and as such they are subject to information loss from whatever dimensionality reduction method is used, which in our case is PCA. The following is the PCA variance explained for each method:
- Contrastive Pairs: 45%
- Contrastive Triplets: 56%
- NT-Xent: 35%
- Cross-entropy: 80%
The representations we get from Triplet Loss appear better suited to reduction by PCA (compared to the other contrastive losses), which might explain some of the nice plots we’re getting. The representations from Contrastive Pairs and NT-Xent could contain more information and be better decorrelated in the features, which would make this a poor plot to use alone to judge representation quality. In addition, there’s many other questions these plots don’t answer:
Which one of these is the best for downstream tasks? Do one of these loss functions generate an embedding space that is linearly separable in the classes? Are the same classes close in each of these embedding spaces (nearest neighbors) or are the locations randomized? Do the intra-class placements make semantic sense?
There are a few different techniques we can utilize to answer these questions. The techniques broadly fall into three different areas:
- Cluster analysis [Silhouette Coefficient, Rand Index, Mutual Information]
- Dimensionality reduction [PCA, T-SNE]
- Linear classification [Linear probe]
Measuring the quality of the embedding space will largely be the topic of the next part in this series. Once we understand how to measure performance, we will move onto advanced topics like fully self-supervised learning (SimCLR, MoCo, BYOL etc.), the effect of augmentations, hard-negative mining, and decorrelating feature vectors. Stay tuned!
